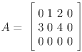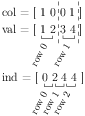Sparse Matrix Formats

[THIS SECTION IS VERY DETAILED AND IS PROBABLY NOT INTENDED FOR THE COMMON USER]

This section describes the sparse matrix storage schemes available in Cysparse. In the next sections, we cover sparse matrix creation, population, view and conversion.

Basically, we use one general sparse matrix format to create a general sparse matrix: the LLSparseMatrix class. This class has a rich API and allows multiple ways to create and transform a sparse matrix. Once the matrix is ready to be used, it can be appropriately converted into a specialized sparse matrix format that is optimized for the needed operations. The LLSparseMatrix is also the only type of matrices that can be modified while the other types of matrices are immutable for efficiency.

Here is a list of existing formats and their basic use:

• Linked-list format (LL): a convenient format for creating and populating a sparse matrix, whether symmetric or general.
• Compressed sparse row format (CSR): a format designed to speed up matrix-vector products.
• Compressed sparse column format (CSC): a format designed to speed up vector-matrix products.

The CSR and CSC formats are complementary and can be viewed as respectively a row- and column view of a sparse matrix.

These formats are well known in the community and you can find scores of documents about them on the internet.

Sorted column and row indices

[TO BE WRITTEN]

For all sparse matrix formats, we internally keep the indices sorted, i.e. in ascending order.

The LL sparse format in details

This format is implemented by the LLSparseMatrix class.

All matrix classes are straightforward with perhaps the only exception of the LLSparseMatrix class. This class is really a container where you can easily add or remove elements but it is not much more than that: a container. As such, it is not optimized for any matrix operation. There are some internal optimisations though to add or retrieve an element and we explain them here.

Elements are linked in chains (aka linked lists)

The LLSparseMatrix container is made of 4 one dimensionnal arrays and one pointer (free):

• root[i]: points to the first elements of row i;
• col[k]: contains the column index j of an element stored at the k-th place;
• val[k]: contains the value of the element stored at the k-th place;
• link[k]: contains the pointer to the next element in the chain where the k-th element belongs.

The pointer free points to the first free element in the chain of free elements.

Despite its name, linked list sparse matrix, this container doesn’t use list of pointers but only arrays of indices. “Pointers” are indices in arrays and to denote a pointer to NULL the value -1 if used. For instance, if free == -1, this means that the chain of free elements is empty.

Then chain can be traversed by following the link array:

Chains in an LLSparseMatrix matrix

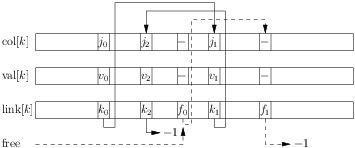
Two chains are depicted in the picture. First, the chain with free elements. These are elements that where removed. The free pointer points to the first element of this chain and link[free] if \(f_0\) which points to the second element in this chain. Whenever a new elements is added, it will take the place of this first element.

The second chain starts with element (\(j_0\), \(v_0\), \(k_0\)). \(k_0\) points to the second element (\(j_1\), \(v_1\), \(k_1\)) and \(k_1\) points to the second and last element (\(j_2\), \(v_2\), \(k_2\)).

Inside the arrays, the elements can be stored in any order.

Elements are “aligned” row wise (chains correspond to rows)

Each chain of elements corresponds to one row of the matrix. The pointer root[i] points to the first element of the i ^th row. If the above chain (\(k_0\), \(k_1\) and \(k_2\) ) correspond to the only elements on row i, root[i] would point to element (\(j_0\), \(v_0\), \(k_0\)). If row i doesn’t have any element, root[i] == -1.

To traverse the i^th row, simply use:

k = self.root[i]

while k != -1:
    # we consider element A[i, j] == val
    j = self.col[k]
    val = self.val[k]
    ...
    k = self.link[k]

Inside a row, elements are ordered by column order (how to run through a LL matrix)

If the chain corresponding to row i is \(k_0, k_1, \ldots, k_p\), then we know that the corresponding column indices are ordered: \(j_0 < j_1 < \ldots < j_p\). When an element is added with the put(i, j, val) method, this new element is inserted in the right place, swapping pointers elements of link if necessary.

This means that looking for an element A[i, k], one can simply use:

k = self.root[i]

while k != -1:

    if self.col[k] > j:
        # element doesn't exist
        break

    if self.col[k] == j:
        # element exists
        ...

    k = self.link[k]

Insertion of a new element in more details

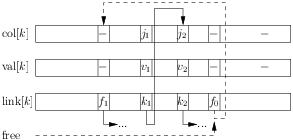
The next figure represent the internal state of a LLSparseMatrix:

Before insertion of element \((j, v, k)\) in a LLSparseMatrix matrix

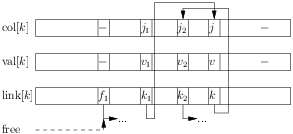
We have \(j_1 < j_2\) and \(k_1\) points to element \(k_2\). Let’s say we want to insert an new element \((j, v, k)\) with column index \(j\) such that \(j_1 < j < j_2\). To preserve the ordering, we have to insert this element between the elements \(k_1\) and \(k_2\) as shown on the following figure:

After insertion of element \((j, v, k)\) in a LLSparseMatrix matrix

The element \((j, v, k)\) was inserted in place of the first free element pointed by free and \(k_1\) now points to this element. Notice also that now, free points to the next free element \(f_1\).

Detailed example

For all sparse matrix formats, we’ll detail an example. Let \(A\) be the following \(3 \times 4\) sparse matrix:

The example sparse matrix \(A\)

Notice that this matrix is sparse with 4 non zero entries, is non symmetric and has an empty row and column.

How to run through a LL matrix

To find all triplets \((i, j, v)\):

for i from 0 <= i < nrow:
    k = self.root[i]
    while k != -1:
       j = self.col[k]
       v = self.val[k]

       k = self.link[k]

The CSR sparse format in details

This format is implemented by the CSRSparseMatrix class. This format use a row-wise representation, as the above LL Sparse format, i.e. elements are stored row by row.

Detailed example

Here are the three internal arrays for the example matrix:

The internal arrays of a CSR matrix

One can immediatly see that the values are stored row-wise in col and val: first the row 0, than the row 1 (and nothing for row 2). ind gives the first indices for each row: ind[0] == 0 gives the start of row 0, ind[1] == 2 gives the start of row 1, etc. This means that ind[i+1] - ind[i] returns the number of elements in row i.

How to run through a CSR matrix

To find all triplets \((i, j, v)\):

for i from 0 <= i < nrow:
    for k from ind[i] <= k < ind[i+1]:
        j = col[k]
        v = val[k]

The CSC sparse format in details

This format is implemented by the CSCSparseMatrix class.

The CSC sparse matrix format is exactly the same as the CSR sparse matrix format but column-wise. Given a matrix \(A\) and a CSR representation of this matrix is exactly the same as a CSC respresentation of the transposed matrix \(A^t\), i.e.

\[\textrm{CSR}(A) = \textrm{CSC}(A^t)\]

and everything we wrote about the CSR format transposes to the CSC format by exchanging rows for columns and vice-versa.

Detailed example

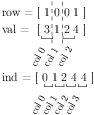
Here are the three internal arrays for the example matrix:

The internal arrays of a CSC matrix

The values are stored column-wise in row and val: first the column 0, than column 1 and finally column 2 (nothing for column 3). ind gives the first indices for each column: ind[0] == 0 gives the start of column 0, ind[1] == 1 gives the start of column 1, etc. This means that ind[j+1] - ind[j] returns the number of elements in column j.

How to run through a CSC matrix

To find all triplets \((i, j, v)\):

for j from 0 <= j < ncol:
    for k from ind[j] <= k < ind[j+1]:
        i = row[k]
        v = val[k]