Introduction¶
NLP.py is a Python package for numerical optimization. It aims to provide a toolbox for solving linear and nonlinear programming problems that is both easy to use and extensible.
NLP.py combines the capabilities of the mature AMPL modeling language with the high-quality numerical resources and object-oriented power of the Python programming language. This combination makes NLP.py an excellent tool to prototype and test optimization algorithms, and also a great teaching aid for optimization.
NLP.py can read optimization problems coded in the AMPL modeling language. All aspects of a problem can be examined and the problem solved. Individual objective and constraint functions, together with their derivatives (if they exist) can be accessed transparently through an object-oriented framework.
NLP.py is extensible and new algorithms can be built by assembling the supplied building blocks, or by creating new building blocks. Existing building blocks include procedures for solving symmetric (possibly indefinite) linear systems via symmetric factorizations or preconditioned iterative solvers, iterative methods for linear least-squares problems, minimization methods for constrained and unconstrained optimization, and much more.
Overview¶
NLP.py is a collection of tools and interfaces for implementing and prototyping optimization algorithms. It is a set of Python modules and classes that support sparse matrices, nonlinear optimization methods, and the efficient solution of large sparse linear systems, especially those occuring in the course of optimization algorithms (e.g., symmetric indefinite systems).
The purpose of NLP.py is to offer an environment in which implementing, testing, prototyping, experimenting with, and modifying and creating innovative optimization algorithms for large-scale constrained problems is a moderately easy task. We feel that the environment should be useful, simple, and intuitive enough that programmers need only concentrate on the logic of the algorithm instead of the intricacies of the programming language. We believe that NLP.py is appropriate for teaching, for learning, and also for bleeding edge research in large-scale numerical optimization. This is achieved by providing the heavy-duty number-crunching procedures in fast, low-level languages such as C, Fortran 77, and Fortran 90/95.
NLP.py aims to
- represent the bleeding edge of research in numerical (differentiable or not) optimization,
- provide a number of low-level tools upon which algorithms may be built, with the intent of solving potentially large problems,
- use sparse matrix data structures to do so,
- provide tools that are useful in the assessment of the performance of optimization algorithms.
Structure of NLP.py¶
NLP.py may be viewed as a collection of tools written in Python and interfaces to core libraries written with the Cython extension of Python. Cython is a superset of Python that facilitates interfacing with libraries that expose a C API and allows users to type variables. Because Cython code is compiled, it results in increased performance, yet remains easier to maintain and update than C or C++. Thanks to the strong connection between Python and Cython, core libraries appear transparently to the user as regular Python objects.
A solid sparse linear algebra library is essential if one is to solve large-scale sparse problems efficiently. The library of choice in NLP.py is CySparse, but several other libraries are also supported to varying degrees.
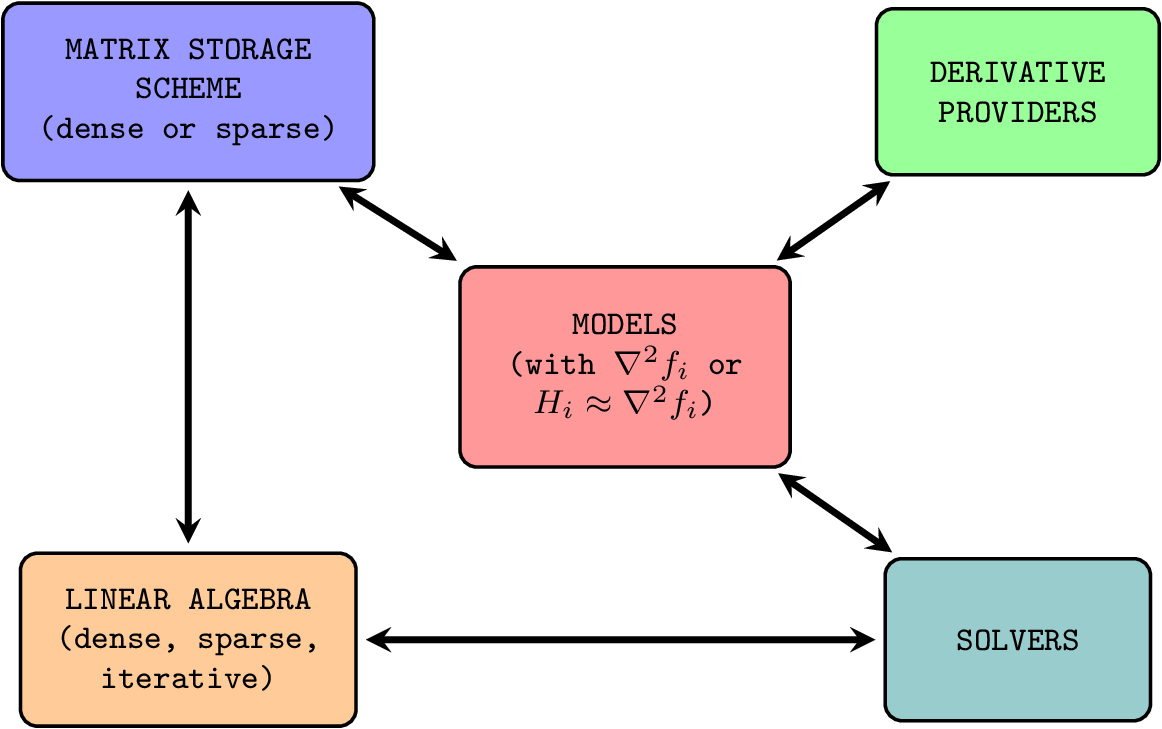
The components of NLP.py revolve around the main tasks with which one is confronted in both modeling and algorithmic design:
Supplying derivatives¶
The first important decision about a model is whether derivatives are available and in the affirmative, whether they will be implemented by hand, supplied by an automatic differentiation engine, or approximated using, say, finite differences or a quasi-Newton scheme.
Matrix storage schemes¶
If it is anticipated that a solver will require Jacobians and/or Hessians, a user must decide how they should be stored—e.g., as dense arrays, sparse matrices in a specific storage format, or implicitly as linear operators. The choice of storage scheme is closely related to what types of operations a solver will need to perform with matrices, e.g., construct block saddle-point systems, and what linear algebra kernels will be used during the iterations.
Modeling¶
Models are represented as Python objects that derive from one or two base classes. The object-oriented design of NLP.py dictates that a model results by inheritance from a model class defining the provenance of derivatives with another model class specifying a matrix storage scheme. For instance, multiple model classes obtain their derivatives from ADOL-C—one per matrix storage scheme—and all derive from a base class named AdolcModel. Similarly, multiple model classes store matrices according to one of the formats available in the CySparse library—one per derivative provider, and all derive from a base class named CySparseModel. For instance, a CySparseAdolcModel class could be defined as inheriting from both AdolcModel and CySparseModel.
Passing models to solvers¶
The choice of a solver depends on multiple factors, including the matrix storage scheme, but more importantly, the structure of the problem. In NLP.py, several solvers are available and correspond to several types of problems. There are solvers for unconstrained optimization, linear and convex quadratic optimization, equality-constrained convex or nonconvex optimization, problems with complementarity constraints, and general problems featuring a mixture of equality constraints, inequality constraints and bounds. A main driver that may be called from the command line is supplied with each solver for problems written in the AMPL modeling language. The PyKrylov companion package supplies several iterative solvers for linear least-squares problems, including regularized problems and problems with a trust-region constraint.
Designing solvers¶
Optimization researchers must often make implementation choices that strike a balance between performance, adherence to theoretical requirements and ease of implementation. An example that comes to mind is a linesearch-based method in which the search must ensure satisfaction of the strong Wolfe conditions. Implementing such a linesearch is far more involved than implementing a simple Armijo backtracking search. The latter may not satisfy the assumptions necessary for convergence, but may still perform well in practice. Similarly, a trust-region method that relies on models using exact second derivatives may perform well, but what if a quasi-Newton approximation is used instead? What if we wish to terminate the iterations early if a condition depending on external factors is satisfied? What if we wish to experiment with a different merit function? It seems important for researchers to be able to experiment easily and swap a linesearch procedure for another, swap a model with exact second derivatives for a quasi-Newton model, and so forth.