Tools

Conversion

Conversion tools from coord format to CSC and vice versa.

hsl.tools.conversion.coord2csc(ncol, irow, jcol, val=None)

Convert a sparse matrix in triple format into CSC format.

To convert to compressed sparse row (csr) format, substitute the number of rows for ncol and swap irow and jcol.

Arguments:

ncol:Number of columns in the input matrix. irow:Integer Numpy array of length nnz containing the row indices of the nonzeros. jcol:Integer Numpy array of length nnz containing the column indices of the nonzeros.

Keywords:

val:Numpy array of length nnz containing the numerical values.

Returns:

rowind:Integer Numpy array of length nnz containing the row indices of the nonzeros in each column. colptr:Integer Numpy array of length ncol+1 containing the positions in rowind of the start of each column. values:Numpy array of length nnz containing the numerical values.

hsl.tools.conversion.csc2coord(rowind, colptr)

Convert a sparse matrix in CSC format into triple format.

To convert to compressed sparse row (csr) format, swap irow and jcol.

Arguments:

rowind:Integer Numpy array of length nnz containing the row indices of the nonzeros in each column. colptr:Integer Numpy array of length ncol+1 containing the positions in rowind of the start of each column.

Returns:

irow:Integer Numpy array of length nnz containing the row indices of the nonzeros. jcol:Integer Numpy array of length nnz containing the column indices of the nonzeros.

Matrix readers

Harwell-Boeing and Rutherford-Boeing matrix format reader.

Provides access to sparse linear systems described in Harwell-Boeing or Rutherford-Boeing format. This module exposes the two classes HarwellBoeingMatrix and RutherfordBoeingData. For more information, see the references below.

References

[DGL]

I.S. Duff, R.G. Grimes and J.G. Lewis, Sparse Matrix Test Problems, ACM Transactions on Mathematical Software, 15(1), p.1-14, 1989

[HBUG]

ftp://ftp.cerfacs.fr/pub/algo/matrices/harwell_boeing/userguide.ps.Z

[HB]	http://math.nist.gov/MatrixMarket/data/Harwell-Boeing

[RBC]

The Rutherford-Boeing Sparse Matrix Collection, I.S. Duff, R.G. Grimes and J.G. Lewis, Technical Report RAL-TR-97-031, Rutherford Appleton Laboratory, Chilton, OX, UK, 1997. (ftp://ftp.numerical.rl.ac.uk/pub/reports/duglRAL97031.pdf)

[RB]	http://www.cerfacs.fr/algor/Softs/RB

class hsl.tools.hrb.HarwellBoeingMatrix(fname, **kwargs)

Bases: object

Import a sparse matrix from a file in Harwell-Boeing format.

The matrix is stored in compressed sparse row format in (self.ind, self.ip, self.val). Right-hand sides, if any, are stored in self.rhs. Right-hand sides can be stored as dense vectors, in which case self.rhs has shape (nrow, nrhs), as sparse vectors, in which case they are stored in compressed sparse column format in (self.rhsptr, self.rhsind, self.rhs), or in elemental format (typically when the matrix itself is stored in finite-element format), in which case self.rhs has shape (nnzero, nrhs).

Note that the matrix indices are zero-based, i.e., row indices range from 0 through nrow-1 and column indices range from 0 through ncol-1.

The matrix can be subsequently converted to triple format with

(val, row, col) = self.find()

Keywords:

pattern_only:do not read matrix element values (False) read_rhs:read right-hand sides, if any (False) read_guess:read starting guess, if any (False) realSol:read solution vector, if any (False)

data()

Return matrix data in compressed sparse row format.

Returns:

val:array of values of nonzero elements ip:array of pointer to rows ind:array of indices of nonzero elements in each row

find()

Return matrix data in coordinate format.

Returns:

val:array of values of nonzero elements irow:array of indices of nonzero elements in each row jcol:array of indices of nonzero elements in each column

class hsl.tools.hrb.RutherfordBoeingData(fname, **kwargs)

Bases: hsl.tools.hrb.HarwellBoeingMatrix

Imports data from a file in Rutherford-Boeing format.

The data is held in (self.ind, self.ip, self.val). If the data represents a sparse matrix, the three arrays represent the matrix stored in compressed sparse row format. Otherwise, the three arrays represent the supplementary data. Refer to the Rutherford-Boeing documentation for more information (reference [4] in the docstring for the present module.)

Note that the matrix indices are zero-based, i.e., row indices range from 0 through nrow-1 and column indices range from 0 through ncol-1.

The data can be subsequently converted to triple format with

(val, row, col) = self.find()

Keywords:

pattern_only:do not read data values (False) transposed:

data()

Return matrix data in compressed sparse row format.

Returns:

val:array of values of nonzero elements ip:array of pointer to rows ind:array of indices of nonzero elements in each row

find()

Return matrix data in coordinate format.

Returns:

val:array of values of nonzero elements irow:array of indices of nonzero elements in each row jcol:array of indices of nonzero elements in each column

Read a sparse matrix in Matrix Market format.

See http://math.nist.gov/MatrixMarket for a description of this format.

class hsl.tools.mtx.MatrixMarketMatrix(fname, **kwargs)

A MatrixMarketMatrix object represents a sparse matrix read from a file.

This file must describe a sparse matrix in the MatrixMarket file format.

See http://math.nist.gov/MatrixMarket for more information.

Example: mat = MatrixMarketMatrix(‘1138bus.mtx’)

find()

Return the sparse matrix in triple format (val,irow,jcol). If the matrix data type is None, i.e., only the matrix sparsity pattern is available, this method returns (irow,jcol).

Sparsity pattern

Plot the sparsity pattern of a sparse matrix.

hsl.tools.spy.spy(A, patternonly=True, **kwargs)

Plot the sparsity pattern of a sparse matrix object.

The sparse matrix object must implement find(), which must return the contents of the matrix in coordinate format, i.e., (val,irow,jcol).

Parameters:

A:Input matrix patternonly:If True, only output a black and white sparsity pattern. If False, colorize the plot according to the magnitude of the nonzero elements.

Keywords:

ax:A Pylab Axes instance used to plot the sparsity pattern. If none is given, this function returns an Axes instance. title:String to be used as title for the plot. If none is given, the title defaults to giving the order of the matrix and the number of nonzero elements. comment:Comment to be appended to the default plot title in case no title is supplied. showtitle:Show or hide plot title.

hsl.tools.spy.fast_spy(nrow, ncol, irow, jcol, **kwargs)

Plot the sparsity pattern of a sparse matrix in coordinate format.

Parameters:

nrow:Number of rows of the matrix. ncol:Number of columns of the matrix. irow:Integer Numpy array of length nnz giving the row indices of the nonzero elements. jcol:Integer Numpy array of length nnz giving the column indices of the nonzero elements.

Keywords:

ax:A Pylab Axes instance used to plot the sparsity pattern. If none is given, this function returns an Axes instance. sym:Should be set to True if the matrix is symmetric and only one triangle is passed in (irow,jcol). title:String to be used as title for the plot. If none is given, the title defaults to giving the order of the matrix and the number of nonzero elements. comment:Comment to be appended to the default plot title in case no title is supplied. showtitle:Show or hide plot title. val:Float Numpy array of length nnz giving the values of the nonzero elements of the matrix. If supplied, a scatter plot is produced with patches of size proportional to the magnitude of the element. This option can slow down the plot for large values of the number of nonzero elements.

Example

"""Illustrate usage of Harwell-Boeing or Rutherford-Boeing readers and mc21.

Supply a file name as input argument on the command line and uncomment below as
appropriate.
"""

import sys
from hsl.ordering.mc21 import nonzerodiag
from hsl.tools.hrb import HarwellBoeingMatrix, RutherfordBoeingData

if len(sys.argv) < 2:
    sys.stderr.write('Supply input matrix as argument\n')
    sys.exit(1)

fname = sys.argv[1]
# M = HarwellBoeingMatrix(fname, patternOnly=True, readRhs=False)
M = RutherfordBoeingData(fname, patternOnly=True, readRhs=False)

if M.nrow != M.ncol:
    sys.stderr.write('Input matrix must be square\n')
    sys.exit(1)

perm, nzdiag = nonzerodiag(M.nrow, M.ind, M.ip)
print 'Number of nonzeros on diagonal after reordering: ', nzdiag

try:
    from hsl.tools.spy import fast_spy
    import pylab
    (_, irow, jcol) = M.find()
    left = pylab.subplot(121)
    fast_spy(M.nrow, M.ncol, irow, jcol, sym=M.issym, ax=left.get_axes())

    right = pylab.subplot(122)
    fast_spy(M.nrow, M.ncol, perm[irow], jcol, sym=M.issym, ax=right.get_axes())
    pylab.show()
    # pylab.savefig('mc21.pdf', bbox_inches='tight')

except:
    pass

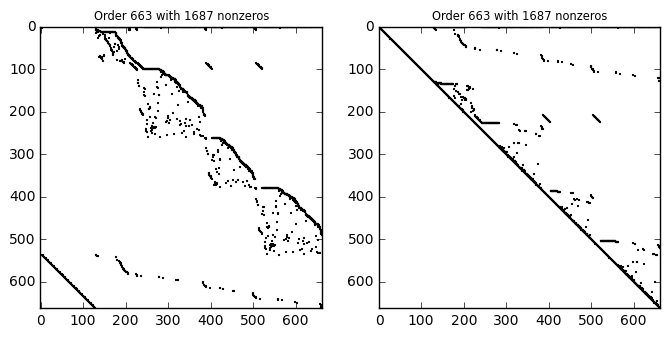
The sparsity pattern of the orginal matrix is shown on the left plot. The right plot show sthe same matrix after usage of the nonzerodiag function which attempts to find a row permutation so the row-permuted matrix has a nonzero diagonal, if this is possible.